What Is The Reference Angle For 5Pi 3

What Is The Reference Angle For 5Pi 3 - The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. Here, we can clearly see that. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The angle is, ⇒ 5π / 3. Therefore the correct option is b. Given, angle in radians = 5π/3. The reference angle for 5π/3 is π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. The reference angle of 3π/4 will be π/3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal.

The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. The reference angle for 5π/3 is π/3. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Here, we can clearly see that. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. The reference angle of 3π/4 will be π/3. The angle is, ⇒ 5π / 3. Therefore the correct option is b. Given, angle in radians = 5π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full.

The reference angle for 5π/3 is π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The reference angle of 3π/4 will be π/3. Here, we can clearly see that. The angle is, ⇒ 5π / 3. Therefore the correct option is b. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Given, angle in radians = 5π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full.

pi/3 is the reference angle for A. 2pi/3 B. 15pi/3 C. 7pi/3 D. 19pi/3

The angle is, ⇒ 5π / 3. The reference angle for 5π/3 is π/3. Therefore the correct option is b. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Here, we can clearly see that.

Ex Sine And Cosine Values Using The Unit Circle Multiples, 54 OFF

Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The reference angle of 3π/4 will be π/3. The angle is, ⇒ 5π / 3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Given, angle in radians = 5π/3.

inverse trigonometric functions and reference angles for the following

To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Therefore the correct option is b. The reference angle of 3π/4 will be π/3. Given, angle in radians = 5π/3. The angle is, ⇒ 5π / 3.

Angle Of Rotation Examples

The reference angle for (5pi)/4 is pi/4 , which has a terminal point of

Here, we can clearly see that. The reference angle for 5π/3 is π/3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. The latter is known as the vertex of the angle and the rays as the sides, sometimes.

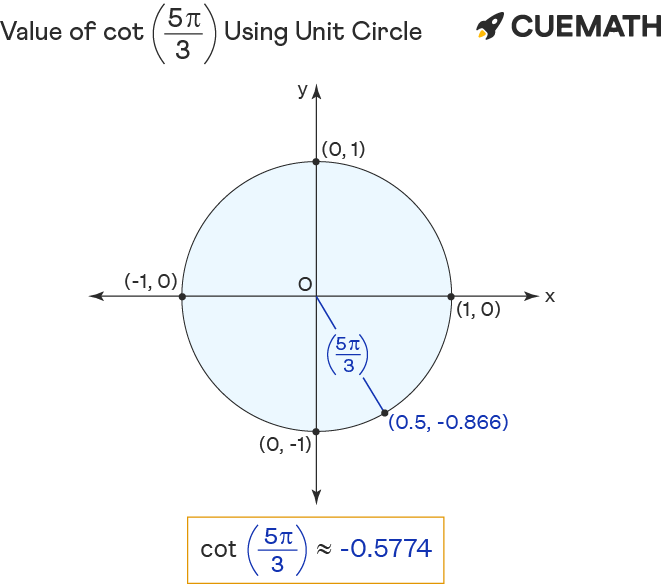
Cot 5pi/3 Find Value of Cot 5pi/3 Cot 5π/3

The reference angle for 5π/3 is π/3. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Therefore the correct option is.

What is the reference angle and cosine of StartFraction 7 pi Over 6

The angle is, ⇒ 5π / 3. The reference angle of 3π/4 will be π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Given, angle in radians = 5π/3.

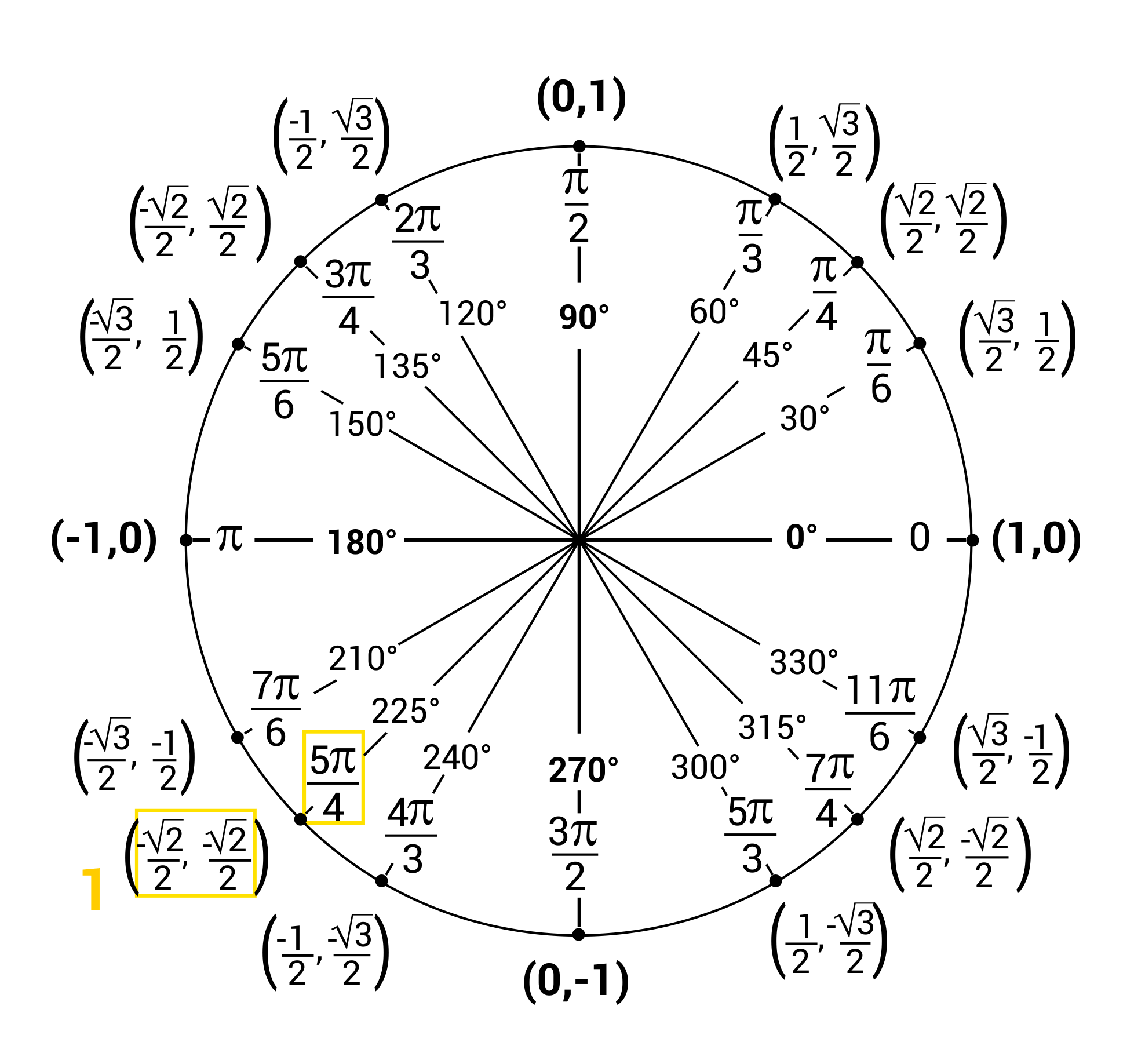
Unit Circle Practice Worksheets

Here, we can clearly see that. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Given, angle in radians = 5π/3. The reference angle for 5π/3 is π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the.

for this special angle, draw the angle and find the reference angle t

Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Here, we can clearly see that. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. The reference angle for 5π/3 is.

Reference Angles NBKomputer

The reference angle of 3π/4 will be π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. The reference angle for 5π/3 is π/3. The angle is, ⇒ 5π / 3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is.

Here, We Can Clearly See That.

The reference angle for 5π/3 is π/3. Given, angle in radians = 5π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. Therefore the correct option is b.

The Angle 5Pi/3 Is In The Fourth Quadrant (Meaning Cosine Is Positive While Sine & Tangent Are Negative), And Its Reference Angle Is 60 Degrees With Respect To The Horizontal.

To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. The angle is, ⇒ 5π / 3. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The reference angle of 3π/4 will be π/3.