Elipse Standard Form
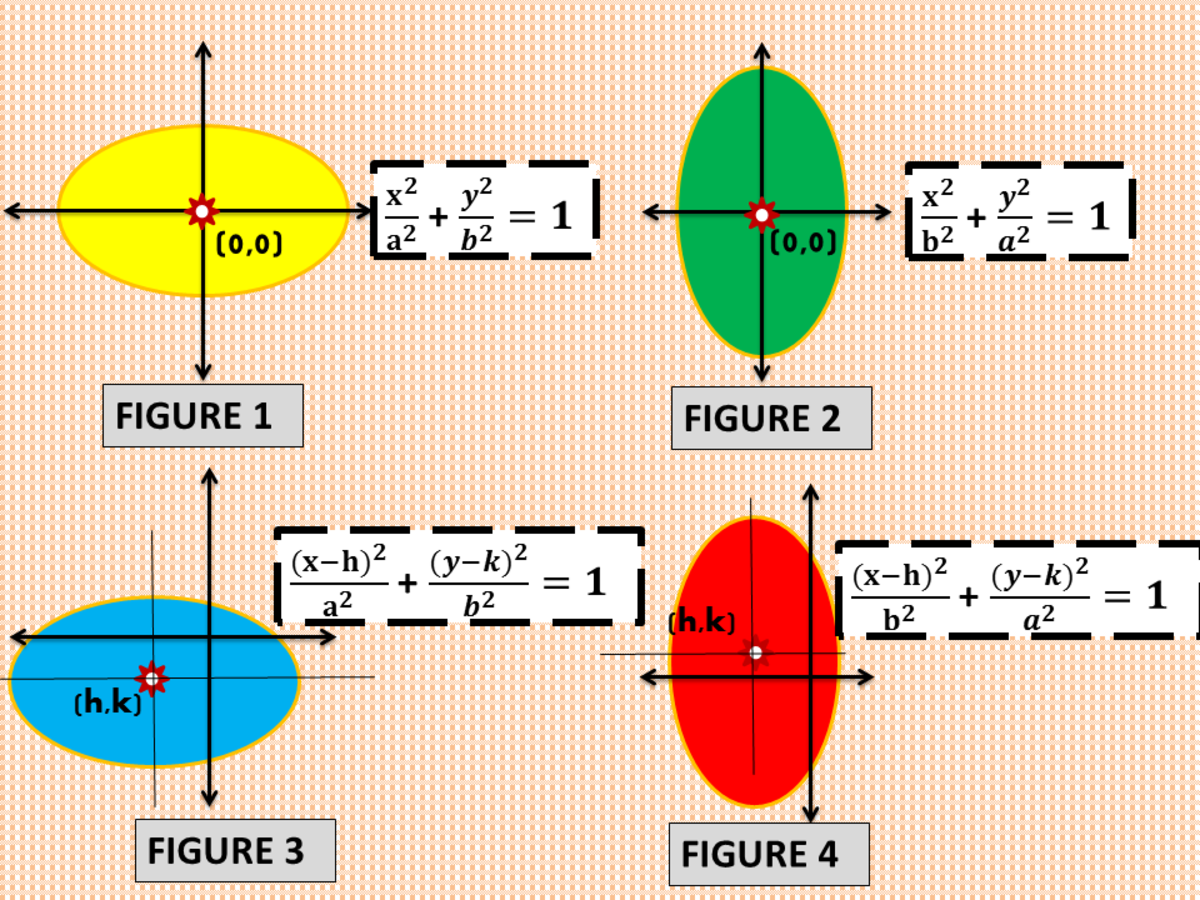
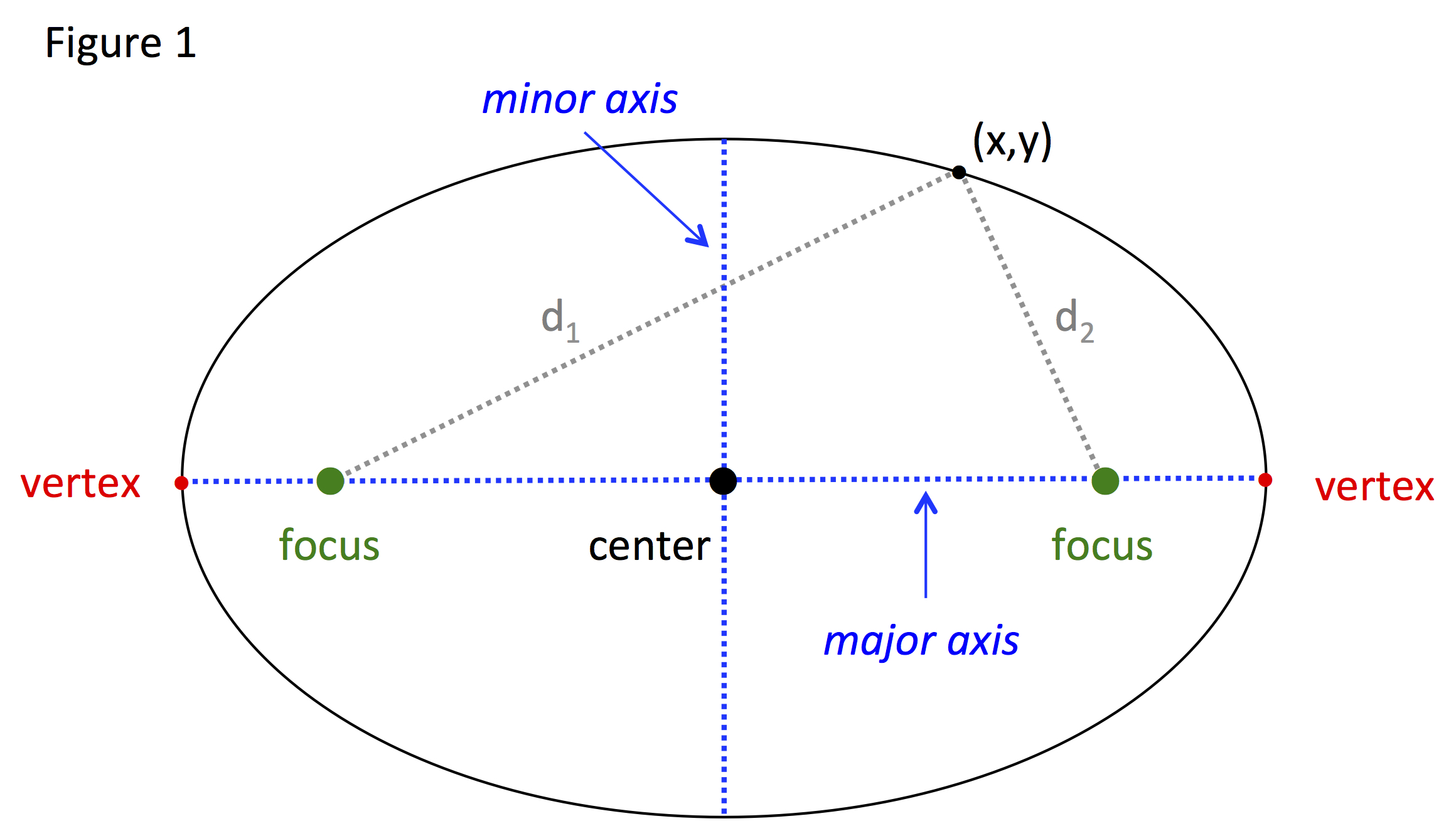
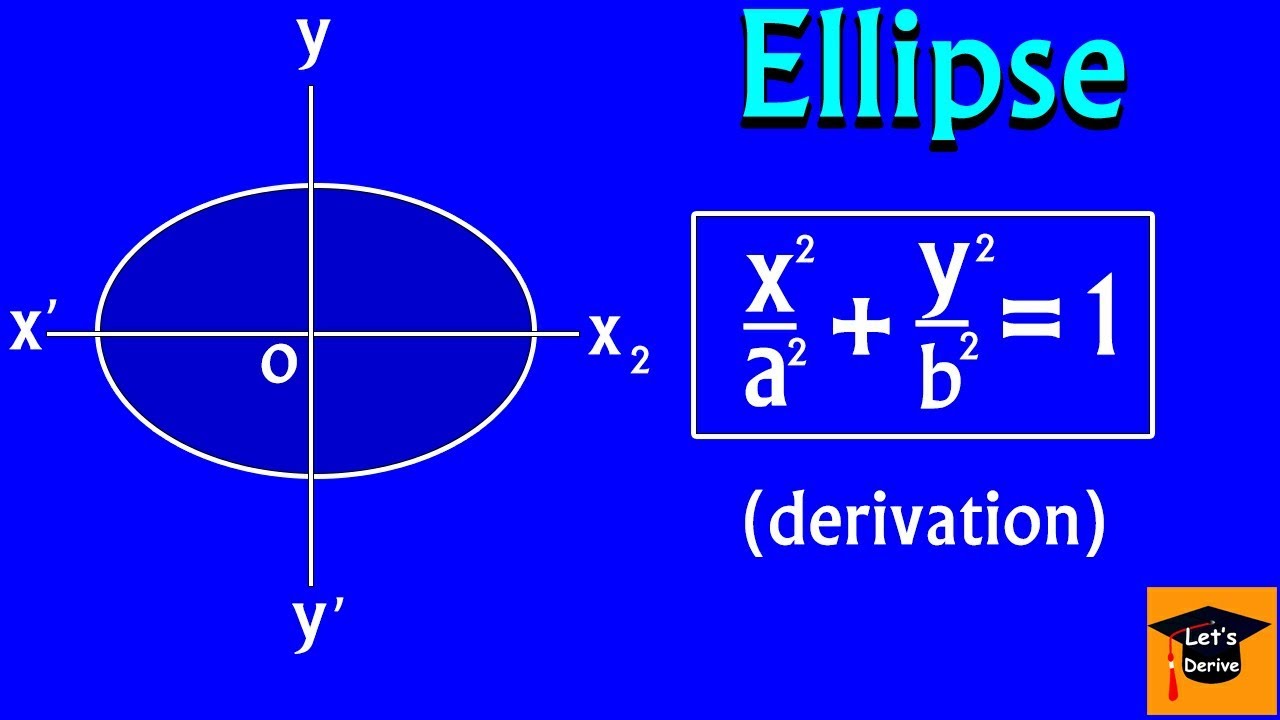
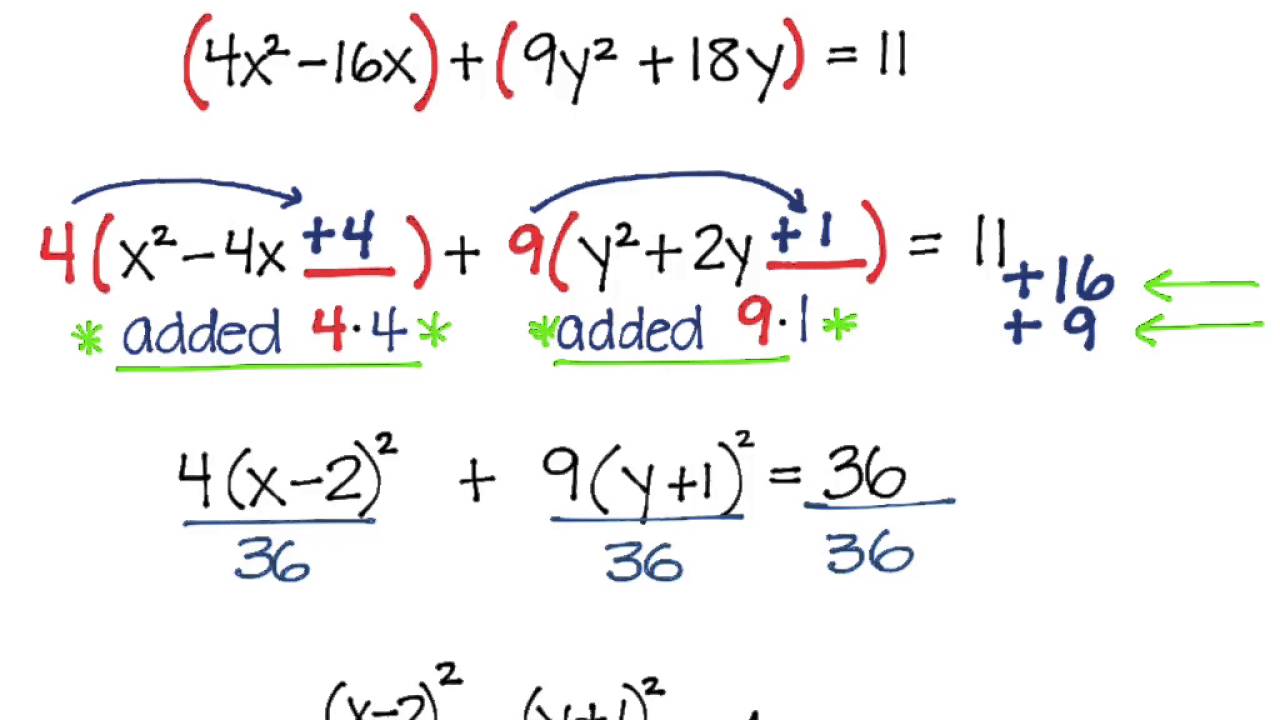Elipse Standard Form - This form can be converted to the. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =.
The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. This form can be converted to the. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1.
The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. This form can be converted to the. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1.
92 Ellipse into standard form from equation YouTube
This form can be converted to the. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}}.
Determine the general form of equation of an elipse whose standard form
First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} =.
How to Graph an Ellipse Given an Equation Owlcation
This form can be converted to the. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The vertex form is \frac {x^ {2}} {9} +.
Ellipse Formula General Form
The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. This form can be converted to the. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The standard form of an ellipse in cartesian coordinates.
Ellipse Standard Equation
The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2.
Conics Standard Form of an Ellipse Expii
First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. This form can be converted to the. The standard form of an ellipse in cartesian coordinates.
Equation Of Ellipse derivation YouTube
The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. This form can be converted to the. The standard form of an ellipse in cartesian coordinates.
ellipse general form to standard form YouTube
The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. This form can be converted to the. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}}.
Ellipse Equation, Properties, Examples Ellipse Formula
The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. First we will learn to derive the equations of ellipses, and then we will learn how to write the.
Writing Equations of Ellipses In Standard Form and Graphing Ellipses
This form can be converted to the. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}}.
First We Will Learn To Derive The Equations Of Ellipses, And Then We Will Learn How To Write The Equations Of Ellipses In Standard Form.
The standard form is \frac {x^ {2}} {3^ {2}} + \frac {y^ {2}} {2^ {2}} = 1 32x2 + 22y2 = 1. The standard form of an ellipse in cartesian coordinates assumes that the origin is the center of the ellipse,. The vertex form is \frac {x^ {2}} {9} + \frac {y^ {2}} {4} = 1 9x2 + 4y2 =. This form can be converted to the.